Inlägg
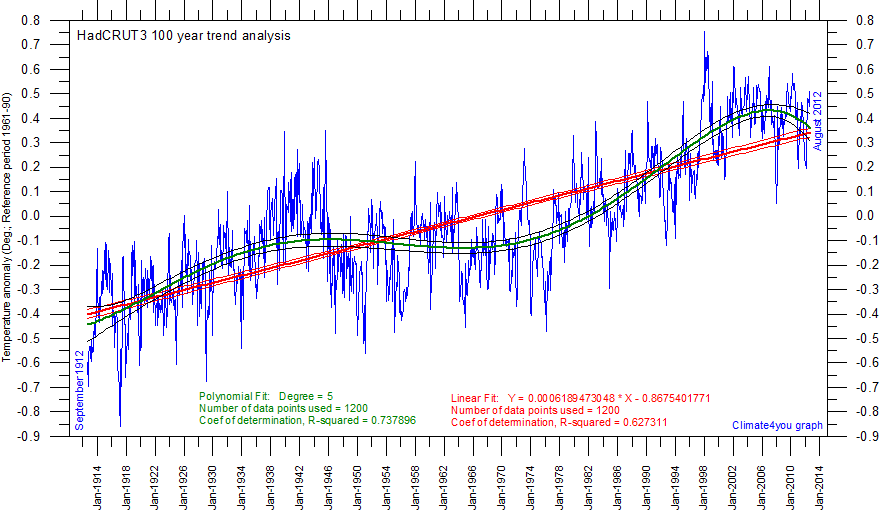
Ovanstående diagram finns på sidan climate4you. Vi ser en tafflig linjär anpassning som inte fångar upp variationerna och en förträfflig anpassning med ett femtegradspolynom. Vi ser också tydligt hur temperaturtrenden vänder mellan 2000-2010 och visar en avkylning. Eller?
Att göra polynomanpassning på ett vettigt sätt är svårare än vad den oerfarna ofta kan tro, speciellt om du använder polynom av högre ordning. Det finns många gropar att falla i. För att illustrera detta kan vi skapa en artificell dataserie utan systematisk förändring, men med rött brus. Hos rött brus är varje datapunkt ett slumptal plus den föregående punkten multiplicerad med en konstant (xn=axn-1+rand). Rött brus är en bra beskrivning på många processer i naturen där resultatet beror på dels föregående värde, dels en slumpmässig faktor. En varm dag följs oftare av en varm dag än vad en kall dag gör, men det går inte att uttala sig säkert.
Vilken av anpassningarna gör bästa jobbet här? Vi har ju bestämt att vi inte ska ha något annat än rött brus. Det finns ingen långsiktig utveckling, eller signal, helt enkelt för att data är konstruerade så. I det här fallet är det uppenbart att det är den linjära anpassningen som faktiskt ger den bästa beskrivningen av data. Femtegradsanpassningen hittar signal som inte finns där. Som princip bör du använda linjära anpassningar om data inte uppenbart avviker från dem, vilket inte händer i dessa exempel.
Det är också lockande att tolka in en förutsägelse i femtegradsanpassningen från climate4you. Visst ser vi hur kurvan vänder? Vi kanske kan använda polynomet för att ge oss en bild av vad som kommer hända i framtiden? Vi kan ju kolla både vad den aktuella anpassningen visar och vad en anpassning utförd för femton år sedan skulle ha visat. Om vi hade kollat på femtegradsanpassningar år 1996, hur hade "förutsägelserna" sett ut då?
Femtegradspolynomet "förutsäger" alltså en accelerande avkylning som komme ge två graders avkylning under de närmsta tjugo åren. Går vi ännu längre fram i tiden blir det allt mer dramatiskt. Anpassningen som har 1996 som slutår visar ungefär samma beteende med en accelererande avkylning. Nu har vi ju facit hur det gick och det stämmer som ni vet inte. Även denna övning visar att femtegradspolynom är dåliga på att visa verkliga tendenser hos dataserier.
Men varför använder då climate4you femtegradspolynom? Det kan vi inte veta säkert, men om vi kollar olika polynomgrader får vi en ledtråd.
Den linjära anpassningen är, tja, rätlinjig. Andra-, tredje- och fjärdegradsanpassningarna visar på en accelererad uppvärmning, men femtegradsanpassningen visar en avstanning i slutet. BINGO!
Det är också lockande att tolka in en förutsägelse i femtegradsanpassningen från climate4you. Visst ser vi hur kurvan vänder? Vi kanske kan använda polynomet för att ge oss en bild av vad som kommer hända i framtiden? Vi kan ju kolla både vad den aktuella anpassningen visar och vad en anpassning utförd för femton år sedan skulle ha visat. Om vi hade kollat på femtegradsanpassningar år 1996, hur hade "förutsägelserna" sett ut då?
Men varför använder då climate4you femtegradspolynom? Det kan vi inte veta säkert, men om vi kollar olika polynomgrader får vi en ledtråd.
Man behöver inte ens tänka på vilket polynom de råkar använda. Avstanningen i uppvärmningen från 1998 och framåt kan om man ser på diagrammet vara en tillfällig avvikelse från den längre (linjära) trenden, ungefär som 1945-1951 avvek, eller 1959-1965. Men intressant ändå att se varför de valt just femtegradspolynomet.
SvaraRaderaJepp, flute. Jag visade detta för nästan tre år sedan, men för de som inte vill förstå hjälper det inte.
SvaraRaderaJa, det är inte så att vetenskapligt underlag ställs mot annat vetenskapligt underlag. Vetenskapligt underlag ställs mot CO2-intressen (eller bättre nu och här-intressen) där allt filtreras, vinklas, vrids, förvrängs, kompletteras och formuleras för måluppfyllelse.
SvaraRaderaJag har mailat professor Ole Humlum som driver climate4you med en länk till inlägget och bett honom utvecka varför han använder femtegradsanpassningen.
SvaraRaderaHej Erik
SvaraRaderaMange tak for dit spørgsmål til mig. Det var interessant at høre, at mine grafer benyttes i den svenske klimadebat.
Du spørger hvorfor jeg gør tilpasning med et femtegradspolynom i www.climate4you.com, og vad jeg anser att anpassningen visar?
Forklaringen er ret enkel: Jeg fikk på et tidspunkt indtryk af at mange beregnede lineære trendlinjer på forskjellige dataserier, uden først at vurdere, om disse egentlig grundlæggende viser en lineær udvikling. Personlig mener jeg at en lineær trend kun i begrænset omfang kan siges at beskrive den globale temperaturudvikling 1911-2011. Derfor ønskede jeg at henlede opmærksomheden på at der også findes andre typer tilpasning, eksempelvis polynomial tilpasning.
I forvejen havde jeg det indtryk, at den viste temperaturudvikling muligvis bedre kunne beskrives som resultatet af en gradvis temperaturstigning med en 60-65 års cyklisk variation pålejret. En ca. 60-65 års cyklisk variation kendes jo fra flere forskellige dataserier, bl.a. marinbiologiske, hvorfor det var naturligt at se om den også genfindes i de forskellige globale temperaturestimater?
Derfor besluttede jeg at forsøge en polynomial tilpasning til temperaturserien, og først med et femtegradspolynomie opnåede jeg god tilpasning, som du meget venligt karakteriserer som ‘fortreffelig’. Med laveregradspolynomier er tilpasningen mindre god, som du også viser i en af dine figurer.
Så svaret på dit spørgsmål er at mit diagram viser at det med et femtegradspolynomium er mulig at forestage en god tilpasning til den målte temperaturserie, og langt bedre end det som er muligt med en lineær trendlinje; hverken mere eller mindre.
Med hensyn til at benytte polynomiet til forudsigelse, har det ikke været min hensigt, og jeg har da heller ikke forsøgt det. Men det er en interessant ide som du fremsætter. Det ser jo unægtelig ud til at den omtalte 60-65 års periodiske variation fortsat kan være i funktion? Jeg er dog lidt skeptisk til nytteværdien af en polynomiebaseret forudsigelse alene, og vil nok først anbefale en mere grundig frekvensanalyse af temperaturserien.
Med venlig hilsen, Ole
"Så svaret på dit spørgsmål er at mit diagram viser at det med et femtegradspolynomium er mulig at forestage en god tilpasning til den målte temperaturserie, og langt bedre end det som er muligt med en lineær trendlinje; hverken mere eller mindre."
SvaraRaderaOle H, testa att anpassa ett 13-grads polynom och du kommer att finna en bättre fit än för 5-gradspolynomet, för ett 27-gradspolynom en ännu bättre. Vad drar du för slutsats av det? Och för ett 1199-grads polynom får du en helt perfekt anpassning till punkterna!
Och som ErikS visar så förutsäger 5-gradsanpassningen extremt dåligt på tidigare interval, (sämre än den linjära!). Varför skulle den plötsligt ha något förklaringsvärde efter just 100 år?
Hittar du 60-65 års cykeln innan 1911 också och hur förklarar dina cykler att nivån plötsligt ligger mycket högre än tidigare?
Och vi vet med c:a 100% säkerhet att kurvan signifikant påverkats av bl.a. växthusgaser, aerosoler, solcykel och ENSO så det verkar ganska meningslöst att inte först korrigera för kända variationer i dessa.
"Och vi vet med c:a 100% säkerhet att kurvan signifikant påverkats av bl.a. växthusgaser, aerosoler, solcykel och ENSO så det verkar ganska meningslöst att inte först korrigera för kända variationer i dessa."
SvaraRaderaSå enkelt och så grundläggande! Mästerligt formulerat!
Kurt Persson
Till saken hör att vilken polynomanpassning man än väljer för att ge sken av något man eftersträvar så blir det ändå bara en svängning runt samma linjära förlopp.
SvaraRaderaMatematisk statistik när den används som sämst. Jag skulle snarare föreslå att en markov-process används där man först räknar ut år-till-år spridningen och sedan låter markov-processen iterera tills dess att spridningen mellan mätdata och genererade markov-värden motsvarar spridningen år-till-år / sqrt(2). Den erhållna kurvan är inget polynom alls då, utan en kurva utan matematisk beskrivning som erhålls som ett medelvärde av de stokastiska "hopp" som processen gör under ett stort antal svep genom tidsserien. Den metoden har jag med framgång använt på en mängd olika mätserier med olika ursprung.
SvaraRaderaHumlum tycks ha fått en artikel publicerad med liknande statistiska övningar som ovan. Se här
SvaraRaderaJohan E:
SvaraRaderaRent allmänt kan man säga att ju högre polynom vi väljer, desto bättre kommer observationerna att bli beskrivna. Om vi har n observationer och ett n:te gradens polynom får vi en perfekt anpassning.
Utanför själva observationsområdet kommer dock kurvan att gå rakt uppåt eller rakt nedåt.
Om n är udda börjar kurvan från avgrunden och pekar sedan efter sista observationen rakt uppåt, förutsatt att konstanten framför n är positiv. Om konstanten är negativ blir det tvärtom. För att denna konstant skall bli positivt måste de sista observationerna vara klart större än de första.
Om n är jämnt kommer båda svansarna utanför observationsområdet att peka åt samma håll.
Märk ordet beskrivande i första meningen. Något förklaringsvärde har anpassningarna inte.